6.0 Reaction Kinetics
NOTE: It may appear that there are gaps on your phone, ensure you close each table section for a better scrolling experience!
Candidates should be able to:
(a) explain and use the terms: rate of reaction; rate equation; order of reaction; rate constant; half-life of a reaction; rate-determining step; activation energy; catalysis
(b) construct and use rate equations of the form rate = k[A]m[B]n (limited to simple cases of single-step reactions and of multi-step processes with a rate-determining step, for which m and n are 0, 1 or 2), including: (i) deducing the order of a reaction by the initial rates method (ii) justifying, for zero- and first-order reactions, the order of reaction from concentration-time graphs (iii) verifying that a suggested reaction mechanism is consistent with the observed kinetics (iv) predicting the order that would result from a given reaction mechanism (v) calculating an initial rate using concentration data [integrated forms of rate equations are not required]
(c) (i) show understanding that the half-life of a first-order reaction is independent of concentration (ii) use the half-life of a first-order reaction in calculations
(d) calculate a rate constant using the initial rates method
(e) devise a suitable experimental technique for studying the rate of a reaction, from given information
(f) explain qualitatively, in terms of frequency of collisions, the effect of concentration changes on the rate of a reaction
(g) show understanding, including reference to the Boltzmann distribution, of what is meant by the term activation energy
(h) explain qualitatively, in terms both of the Boltzmann distribution and of collision frequency, the effect of temperature change on a rate constant (and hence, on the rate) of a reaction
(i) (i) explain that, in the presence of a catalyst, a reaction has a different mechanism, i.e. one of lower activation energy, giving a larger rate constant (ii) interpret this catalytic effect on a rate constant in terms of the Boltzmann distribution
(j) outline the different modes of action of homogeneous and heterogeneous catalysis, including: (i) the Haber process (ii) the catalytic removal of oxides of nitrogen in the exhaust gases from car engines (see also Section 11.3) (iii) the catalytic role of atmospheric oxides of nitrogen in the oxidation of atmospheric sulfur dioxide (iv) catalytic role of Fe2+ in the I – /S2O8 2– reaction 9729 H2 CHEMISTRY (2017) 18
(k) describe enzymes as biological catalysts which may have specific activity (l) explain the relationship between substrate concentration and the rate of an enzyme-catalysed reaction in biochemical systems
-
It is the study of the rate and factors that affect a chemical reaction.
-
The reaction mechanism is the sequence of steps in which the reaction occurs.
-
The rate-determining step (RDS) is the slowest step in the sequence.
-
Rate of reaction = change in concentration(moldm^-3)/change in time(s)
Collision Theory
-
To react, particles must collide with each other.
-
They must have sufficient energy to break bonds and be in the correct orientation.
-
An effective collision results in a high energy transition state. (The top of the reaction pathway curve)
-
Bond breaking and forming take place during transition state.
Rate Equation
-
Shows how the rate of a reaction depends on the concentrations of reactants.
-
For a reaction aA + bB = cC + dD
-
Rate = k [A]^m [B]^n , [ ] is concentration.
-
k is a constant. m and n are the orders of reaction with respect to A and B respectively.
-
Unit for the rate is mol dm^-3 s^-1
-
k, m and n are found experimentally and not related to the stoichiometric ratio of the reactants in the equation.
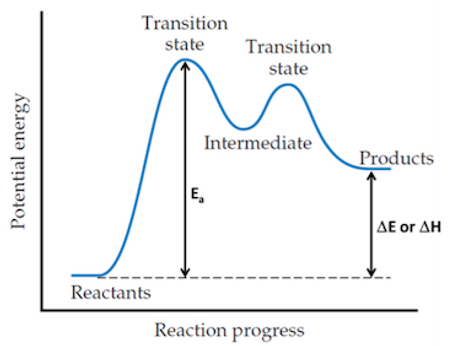
6.1 Reaction Pathway Diagram
-
Ea is the activation energy
-
It is the minimum energy that reactants need to react.
-
It enables bonds to break.
-
Only a small fraction of molecules have energy greater or equal to the Ea.
-
-
Transition State
-
It is the stage where species that are extremely unstable and unable to be isolated are formed.
-
Represents a point of maximum energy in a reaction pathway diagram.
-
-
Intermediate
-
It is the stage where species that are very unstable and that can be isolated for short periods are formed.
-
Represents a point of minimum energy in a reaction pathway diagram.
-
6.2 Rate of Reaction
-
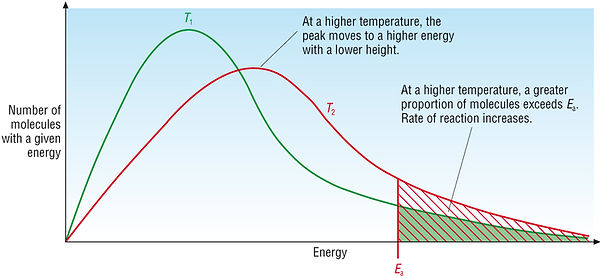
Temperature
-
Increasing temperature increases the average kinetic energy of particles.
-
Particles will move faster and the number of collisions increases.
-
Increased in the number of particles with energies greater or equal to the activation energy of the reaction.
-
-
More effective collisions and rate of reaction increases.
-
-
The concentration of reactants / Pressure of gases
-
Increases concentration of reactants/pressure of gaseous reactants increases the number of reacting particles in the same volume.
-
Particles are closer
-
The frequency of collisions increases
-
Greater chance of effective collisions
-
The rate of reaction increases
-
-
Reactants are consumed gradually during the reaction.
-
Rate gradually decreases (use earlier explanation)
-
Reaction stops when reactants are completely used up.
-
-
The surface area of contact
-
Increasing surface area of contact
-
Increases the amount of reactant exposed to other reactants.
-
Increases the frequency of collisions
-
-
More effective collisions
-
The rate of reaction increases.
-
-
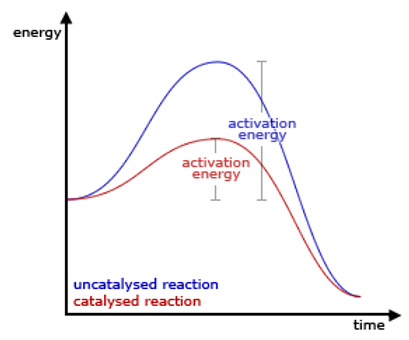
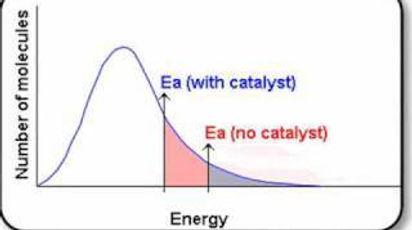
Catalyst
-
A catalyst provides an alternative pathway which has a lower energy barrier for the reaction to take place.
-
More particle will have energies grater or equal to the activation energy of the alternative pathway of reaction.
-
More effective collisions.
-
The rate of reaction increases.
-
The catalyst is regenerated at the end of the reaction.
-
6.3 Order of Reactions
-
For a reaction aA + bB = cC + dD
-
Rate = k [A]^m [B]^n , [ ] is concentration.
-
k is a constant. m and n are the orders of reaction with respect to A and B respectively.
-
k = A*e^(-Ea / RT), A is a pre-exponential factor, Ea is the activation energy, R is gas constant, T is temperature.
-
k is temperature dependent and not affected by changes in concentration.
-
k increases with temperature
-
k increases with the use of a catalyst that provides an alternative pathway of lower activation energy.
-
Zero Order
-
Rate = k
-
The rate of reaction is independent of the concentration of the reactant.

First Order
-
Rate = k[A]
-
Graph of concentration against time
-
Reactant has a constant half-life, Half T = ln (2)/ k
-
Half-life is the time taken for the initial concentration of a reactant to decrease to half of its value.
-
Trick use (Final Amount of Substance) = Initial Amount * (1/2) ^ (Time/Half-life) for half-life questions.
-
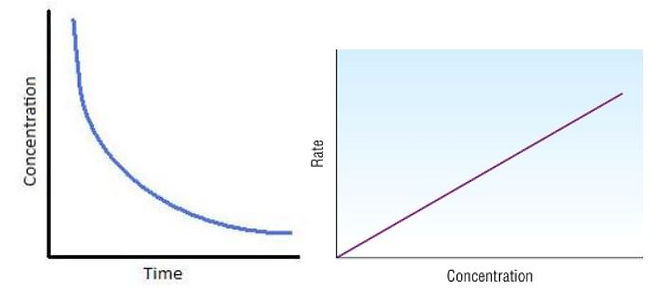
Second Order
-
Rate = k[A]^2
-
Graph of concentration against time
-
Reactant has an increasing half-life
-
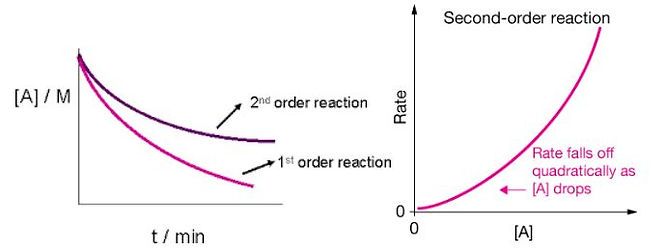
6.4 Determination of Order of Reactions
Chemical reaction: A + B + C = D + E
Rate equation: Rate = k [A]^x [B]^y [C]^z
-
Reactant A
-
Use data from 1 and 2, with [B] and [C] constant. a double increase in the concentration of [A] leads to a double increase in the rate of reaction from r to 2r.
-
It is a first order reaction.
-
-
Reactant B
-
Use data from 1 and 3, with [A] and [C] constant. a double increase in the concentration of [B] leads to a double increase in the rate of reaction from r to 2r.
-
It is a first order reaction.
-
-
Reactant C
-
Use data from 3 and 4, with [A] and [B] constant. a double increase in the concentration of [C] leads to a fourfold increase in the rate of reaction from 2r to 8r.
-
It is a second order reaction.
-
6.4 Experimental Techniques to Study the Rate of Reactions
Titrimetric Method
The concentration of reactants/products is determined at different times by withdrawing known volumes of the reaction mixture and titrating with a suitable standard solution.
Sample volume withdrawn must be quenched by
-
Adding a large volume of cold solvent to slow down the reaction
-
Adding a 'quenching' reagent which would react immediately with one of the reactants to stop the reaction.
Example:
To study the rate of acid-catalysed reaction of propanone with iodine
CH3COCH3(aq) + I2(aq) → CH2ICOCH3(aq) + HI(aq)
-
Determine the amount of unreacted I2(aq) in the reaction mixture at different times.
-
Portions of the reaction mixtures are pipetted at regular time intervals into NaHCO3(aq) which 'quenches' the reaction by neutralising the acid catalyst.
-
The quenched mixture is then titrated against a standard solution of Na2S2O3 to determine the amount of unreacted iodine.
-
The rate of reaction can be found by plotting the graph - the volume of sodium thiosulfate solution against time
Measure of the Volume of Gaseous Product
The volume of gas produced per unit time or loss in mass per unit time may be determined for studying the rate of reaction for reactions involving the formation of the gaseous product.
Example:
To study the rate of reaction between dilute HCl and CaCO3,
2HCl(aq) + CaCO3(s) → CaCl2(aq) + CO2(g) + H2O(l)
-
Determine the volume of CO2 produced per unit time.
-
CO2 is collected in a gas syringe and its volume is measured at regular time intervals.
-
The rate of reaction can be found by plotting the graph - the volume of CO2 against time.
Alternatively, we can determine the loss in mass of flask and its contents per unit time. The rate of reaction can be found by plotting the graph - the mass of conical flask and its contents(g) against time(s).
Colourimetric Method
The colour intensity of a compound is proportional to its concentration, so the rate of reaction may be studied by following the change in colour intensity.
Example:
To study the rate of the acid-catalysed reaction of propanone with iodine
CH3COCH3(aq) + I2(aq) + H+(aq) → CH2ICOCH3(aq) + HI(aq)
-
The rate of reaction can be measured by recording the reduction in the concentration of I2(aq) by the decrease in the intensity of its colour as measured using a colourimeter.
-
The rate of reaction may be found by plotting the graph - colour intensity against time.
Clock Reaction
For reactions that are accompanied by prominent visual changes, the rate of the reaction may be studied by "clock reaction" where the time taken for a prescribed visual change to occur is measured.
Example:
To study the rate of reaction of sodium thiosulfate (VI) with dilute HCl
Na2S2O3(aq) + 2HCl(aq) → S(s) + SO2(g) + 2NaCl(aq) + H2O(l)
-
Measure the time taken for sufficient S(s) to be formed. (Time is taken to obscure a "cross" on the piece of paper)
-
The rate of reaction is inversely proportional to the time taken.
© 2018 Shanmugam Udhaya All Rights Reserved





