4.0 Gaseous State
NOTE: It may appear that there are gaps on your phone, ensure you close each table section for a better scrolling experience!
Candidates should be able to:
Learning Outcomes
Candidates should be able to:
(a) state the basic assumptions of the kinetic theory as applied to an ideal gas
(b) explain qualitatively in terms of inter-molecular forces and molecular size:
(i) the conditions necessary for a gas to approach ideal behavior
(ii) the limitations of ideality at very
high pressures and very low temperatures
(c) state and use the general gas equation pV = nRT
in calculations, including the determination of Mr
(d) use Dalton’s Law to determine the partial pres
sures of gases in a mixture (see also Section 9)
Taken from Chemistry Singapore-Cambridge General Certificate of Education Advanced Level Higher 2 (2019) Syllabus
4.1 States
-
No definite shape
-
No definite volume
-
Low density
-
Low viscosity
-
Far apart from one another
-
Weaker inter-molecular forces of attraction between molecules.
-
Move freely and randomly in all directions at high speed.
4.2 Kinetic Theory
-
Gas particles have negligible size or volume relative to the volume of the container.
-
Negligible intermolecular forces of attraction between gas particles.
-
Gas particles are in continual random motion at high speeds.
-
Collisions are perfectly elastic (No loss in KE)
-
Kinetic energy is directly proportional to temperature. All gas particles have same KE at same temperature.
4.3 Conditions
-
Standard Temperature and Pressure (s.t.p) is 0 °C and 1 bar(100000 Pa). Molar Volume = 22.7 dm^-3
-
Room Temperature and Pressure (r.t.p) is 20 °C and 1atm(101325 Pa). Molar Volume = 24.0 dm^-3
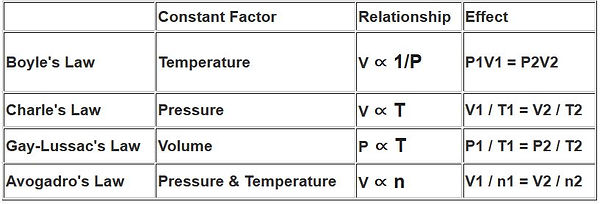
4.4 Gas Laws
Ideal gas Law: pV = nRT **
-
p is the pressure (Pa)
-
V is the volume of the gas (m^3)
-
n is the moles of gas (mol)
-
R is the molar gas constant (8.31 J K^-1 mol^-1)
-
T is the absolute temperature (K) (x °C + 273)
-
A gas that obeys this equation under all conditions is an ideal gas.
-
A real gas is most ideal at high temperature and low pressure.
-
At low pressure, gas particles are widely spaces and hence total volume of gas particles become negligible relative to the volume of the container and IMF forces also become negligible.
-
At high temperatures, gas particles have higher kinetic energy. They can overcome the intermolecular forces of attraction and thus negligible IMF will exist between molecules.
4.5 Limitations of Ideality
-
In a real gas, particles have significant size and there are intermolecular forces of attraction between them.
-
A real gas deviates from ideality at high pressures and low temperatures.
-
At high pressure, gas is compresses and volume of gas decreases and hence total volume of particles becomes significant relative to the size of container.
-
At low temperatures, gas particles have lower KE. They move slower and hence closer together resulting in significant intermolecular forces of attraction.
-
Polar molecules such HCl have stronger IMF than non-polar molecules and hence deviate more from ideality.
-
Large and heavy molecules such as CO2 have significant molecular volume relative to volume of container so they will deviate more from ideality.
4.6 Dalton's Law of Partial Pressure
-
Dalton's Law states that for a mixture of gases that do not react, the total pressure is equal to the sum of partial pressure of each gas.
-
By finding the mole fraction of a specific gas, we can determine the partial pressure of each gas.
4.7 Graphs of Ideal Gas
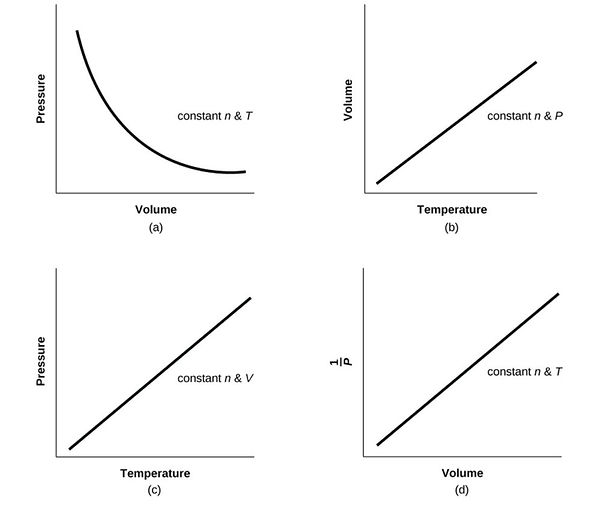

© 2018 Shanmugam Udhaya All Rights Reserved





